Нека е логическа функция от n променливи. Логическото уравнение изглежда така:
Константата C има стойност 1 или 0.
Едно логическо уравнение може да има от 0 до различни решения. Ако C е равно на 1, тогава решенията са всички онези набори от променливи от таблицата на истината, за които функцията F приема стойност true (1). Останалите набори са решения на уравнението с C равно на нула. Винаги можете да разглеждате само уравнения от вида:
Наистина, нека е дадено уравнението:
В този случай можем да отидем до еквивалентното уравнение:
Да разгледаме система от k логически уравнения:
Решението на една система е набор от променливи, за които всички уравнения на системата са удовлетворени. По отношение на логическите функции, за да се получи решение на система от логически уравнения, трябва да се намери набор, върху който логическата функция Ф е вярна, представляваща конюнкция на оригиналните функции:
Ако броят на променливите е малък, например по-малък от 5, тогава не е трудно да се изгради таблица на истината за функцията, която ни позволява да кажем колко решения има системата и какви са наборите, които предоставят решения.
В някои задачи на USE за намиране на решения на система от логически уравнения броят на променливите достига 10. Тогава изграждането на таблица на истината става почти невъзможна задача. Решаването на проблема изисква различен подход. За произволна система от уравнения няма общ метод, различен от изброяването, който позволява решаването на такива проблеми.
В задачите, предлагани на изпита, решението обикновено се основава на отчитане на спецификата на системата от уравнения. Повтарям, освен изпробването на всички опции за набор от променливи, няма общ начин за решаване на проблема. Решението трябва да се изгради въз основа на спецификата на системата. Често е полезно да се извърши предварително опростяване на система от уравнения, като се използват известни закони на логиката. Друга полезна техника за решаване на този проблем е следната. Не се интересуваме от всички множества, а само от тези, на които функцията има стойност 1. Вместо да изграждаме пълна таблица на истината, ще изградим неин аналог - двоично дърво на решенията. Всеки клон на това дърво съответства на едно решение и определя набор, на който функцията има стойност 1. Броят на клоновете в дървото на решенията съвпада с броя на решенията на системата от уравнения.
Ще обясня какво е двоично дърво на решенията и как се изгражда, като използвам примери за няколко проблема.
Проблем 18
Колко различни набора от стойности на логическите променливи x1, x2, x3, x4, x5, y1, y2, y3, y4, y5 има, които удовлетворяват системата от две уравнения?
Отговор: Системата има 36 различни решения.
Решение: Системата от уравнения включва две уравнения. Нека намерим броя на решенията за първото уравнение в зависимост от 5 променливи - . Първото уравнение от своя страна може да се разглежда като система от 5 уравнения. Както беше показано, системата от уравнения всъщност представлява конюнкция на логически функции. Обратното твърдение също е вярно - конюнкция от условия може да се разглежда като система от уравнения.
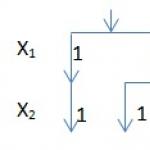
Нека изградим дърво на решенията за импликация () - първият член на конюнкцията, който може да се разглежда като първото уравнение. Ето как изглежда графичното представяне на това дърво

Дървото се състои от две нива според броя на променливите в уравнението. Първото ниво описва първата променлива. Два клона на това ниво отразяват възможните стойности на тази променлива - 1 и 0. На второто ниво клоните на дървото отразяват само онези възможни стойности на променливата, за които уравнението се оценява на истина. Тъй като уравнението определя импликация, клон, който има стойност 1, изисква в този клон да има стойност 1. Клон, който има стойност 0, генерира два клона със стойности, равни на 0 и 1. Конструираната дървото определя три решения, от които импликацията приема стойност 1. На всеки клон се изписва съответен набор от променливи стойности, даващи решение на уравнението.
Тези набори са: ((1, 1), (0, 1), (0, 0))
Нека продължим да изграждаме дървото на решенията, като добавим следното уравнение, следната импликация. Спецификата на нашата система от уравнения е, че всяко ново уравнение на системата използва една променлива от предишното уравнение, добавяйки една нова променлива. Тъй като променливата вече има стойности в дървото, тогава във всички клонове, където променливата има стойност 1, променливата също ще има стойност 1. За такива клонове конструкцията на дървото продължава до следващото ниво, но нови клонове не се появяват. Един клон, където променливата има стойност 0, ще се разклони на два клона, където променливата ще получи стойности 0 и 1. По този начин всяко добавяне на ново уравнение, като се има предвид неговата специфика, добавя едно решение. Оригинално първо уравнение:
има 6 решения. Ето как изглежда пълното дърво на решенията за това уравнение:

Второто уравнение на нашата система е подобно на първото:
Единствената разлика е, че уравнението използва променливи Y. Това уравнение също има 6 решения. Тъй като всяко променливо решение може да се комбинира с всяко променливо решение, общият брой на решенията е 36.
Моля, обърнете внимание, че конструираното дърво на решенията дава не само броя на решенията (според броя на клоните), но и самите решения, записани на всеки клон на дървото.
Проблем 19
Колко различни набора от стойности на логическите променливи x1, x2, x3, x4, x5, y1, y2, y3, y4, y5 има, които отговарят на всички условия, изброени по-долу?
![]()
Тази задача е модификация на предишната задача. Разликата е, че се добавя друго уравнение, което свързва променливите X и Y.
От уравнението следва, че когато има стойност 1 (съществува едно такова решение), то има стойност 1. По този начин има едно множество, на което и има стойности 1. Когато е равно на 0, то може имат произволна стойност, както 0, така и 1. Следователно всеки набор с , равен на 0, и има 5 такива набора, съответства на всичките 6 набора с променливи Y. Следователно общият брой решения е 31.
Проблем 20
Решение: Спомняйки си основните еквивалентности, ние записваме нашето уравнение като:
Цикличната верига от импликации означава, че променливите са идентични, така че нашето уравнение е еквивалентно на уравнението:
Това уравнение има две решения, когато всички са 1 или 0.
Проблем 21
Колко решения има уравнението:
Решение: Точно както в задача 20, преминаваме от циклични импликации към идентичности, пренаписвайки уравнението във формата:
Нека изградим дърво на решенията за това уравнение:

Проблем 22
Колко решения има следната система от уравнения?
Има различни начини за решаване на системи от логически уравнения. Това е свеждане до едно уравнение, изграждане на таблица на истината и разлагане.
Задача:Решете система от логически уравнения:
Нека помислим метод на редукция до едно уравнение . Този метод включва трансформиране на логически уравнения, така че техните десни страни да са равни на стойността на истината (т.е. 1). За да направите това, използвайте операцията за логическо отрицание. След това, ако уравненията съдържат сложни логически операции, ги заместваме с основни: „И“, „ИЛИ“, „НЕ“. Следващата стъпка е да комбинирате уравненията в едно, еквивалентно на системата, като използвате логическата операция „И“. След това трябва да трансформирате полученото уравнение въз основа на законите на логическата алгебра и да получите конкретно решение на системата.
Решение 1:Приложете инверсия към двете страни на първото уравнение:
Нека си представим извода чрез основните операции „ИЛИ“ и „НЕ“:
Тъй като левите части на уравненията са равни на 1, можем да ги комбинираме с помощта на операцията „И“ в едно уравнение, което е еквивалентно на оригиналната система:
![]()
Отваряме първата скоба според закона на Де Морган и трансформираме получения резултат:
Полученото уравнение има едно решение: A =0, B=0 и C=1.
Следващият метод е конструиране на таблици на истината . Тъй като логическите величини имат само две стойности, можете просто да прегледате всички опции и да намерите сред тях тези, за които дадена система от уравнения е изпълнена. Тоест изграждаме една обща таблица на истината за всички уравнения на системата и намираме линия с необходимите стойности.
Решение 2:Нека създадем таблица на истината за системата:
|
0 |
0 |
1 |
1 |
0 |
1 |
Редът, за който са изпълнени условията на задачата, е маркиран с удебелен шрифт. Така че A=0, B=0 и C=1.
начин разграждане . Идеята е да се фиксира стойността на една от променливите (да се зададе равна на 0 или 1) и по този начин да се опростят уравненията. След това можете да коригирате стойността на втората променлива и т.н.
Решение 3:Нека A = 0, тогава:
От първото уравнение получаваме B = 0, а от второто - C = 1. Решение на системата: A = 0, B = 0 и C = 1.
На Единния държавен изпит по информатика много често е необходимо да се определи броят на решенията на система от логически уравнения, без да се намират самите решения; има и определени методи за това. Основният начин за намиране на броя на решенията на система от логически уравнения езаместване на променливи. Първо, трябва да опростите всяко от уравненията възможно най-много въз основа на законите на логическата алгебра и след това да замените сложните части на уравненията с нови променливи и да определите броя на решенията на новата система. След това се върнете към замяната и определете броя на решенията за нея.
Задача:Колко решения има уравнението (A → B) + (C → D) = 1? Където A, B, C, D са логически променливи.
Решение:Нека въведем нови променливи: X = A → B и Y = C → D. Като се вземат предвид новите променливи, уравнението ще бъде написано като: X + Y = 1.
Дизюнкцията е вярна в три случая: (0;1), (1;0) и (1;1), докато X и Y са импликации, тоест тя е вярна в три случая и невярна в един. Следователно случаят (0;1) ще съответства на три възможни комбинации от параметри. Случай (1;1) – ще съответства на девет възможни комбинации от параметри на първоначалното уравнение. Това означава, че общите възможни решения на това уравнение са 3+9=15.
Следващият начин за определяне на броя на решенията на система от логически уравнения е двоично дърво. Нека да разгледаме този метод с пример.
Задача:Колко различни решения има системата от логически уравнения:

Дадената система от уравнения е еквивалентна на уравнението:
(х 1 → х 2 )*(х 2 → х 3 )*…*(x m -1 → x m) = 1.
Нека се преструваме, че х 1 – е вярно, тогава от първото уравнение получаваме това х 2 също вярно, от второто - х 3 =1 и така нататък, докато x m= 1. Това означава, че множеството (1; 1; …; 1) от m единици е решение на системата. Нека сега х 1 =0, тогава от първото уравнение имаме х 2 =0 или х 2 =1.
Кога х 2 true, получаваме, че останалите променливи също са true, т.е. множеството (0; 1; ...; 1) е решение на системата. При х 2 =0 получаваме това х 3 =0 или х 3 = и така нататък. Продължавайки към последната променлива, откриваме, че решенията на уравнението са следните набори от променливи (m +1 решение, всяко решение съдържа m стойности на променливите):
(1; 1; 1; …; 1)
(0; 1; 1; …; 1)
(0; 0; 0; …; 0)
Този подход е добре илюстриран чрез конструиране на двоично дърво. Броят на възможните решения е броят на различните клони на построеното дърво. Лесно се вижда, че то е равно на m +1.
|
Дърво |
Брой решения |
|
|
х 1 |
|
|
|
х 2 |
||
|
х 3 |
||
|
… |
При затруднения в разсъжденията проучване и строителствоот решения, с които можете да търсите решениеизползвайки таблици на истината, за едно или две уравнения.
Нека пренапишем системата от уравнения във формата:

И нека създадем таблица на истината отделно за едно уравнение:
|
х 1 |
х 2 |
(x 1 → x 2) |
Нека създадем таблица на истината за две уравнения:
|
х 1 |
х 2 |
х 3 |
x 1 → x 2 |
x 2 → x 3 |
(x 1 → x 2) * (x 2 → x 3) |
В момента нарастват изискванията за подобряване на качеството на образованието на учениците. Едно от най-важните нововъведения в съдържанието на обучението по математика е включването на елементи от математическата логика в училищните програми. Това се дължи на ролята на логическото знание в общообразователната подготовка на съвременния човек.
Препоръчително е да започнете да изучавате елементите на математическата логика в 5–6 клас или в 7 клас, в зависимост от системата на представяне в учебника, използван за обучение. Необходимото време може да се намери, като се откаже да се разглеждат с ученици въпроси, които не са включени в задължителното минимално съдържание на основното училище (корен от степен n, степен с дробен показател, метод на интервалите, тригонометричен материал в курса по алгебра) , но са запазени в редица учебници и в практиката на учителите.
Но най-често тези раздели се изучават само в избираеми курсове.
Предмет:„Системи логически уравнения” (10 клас)
Цели на урока:
- запознаване на учениците с понятието системи логически уравнения, изучаване на различни методи за решаването им, повтаряне на методи за решаване на алгебрични системи и скаларно произведение на вектори;
- развитие на математическото мислене и логическата реч на учениците, въображението, способността да анализират и прилагат знанията си в непозната ситуация;
- подхранване на интерес към темата, усърдие и внимание.
Оборудване:дъска, тебешир, тетрадки, химикалки, моливи, решетки за решаване на системи с три и четири неизвестни.
ПО ВРЕМЕ НА ЗАНЯТИЯТА
I. Организационен момент
II. Съобщение за темата на урока
Запишете името на темата в тетрадката си.
– В миналия урок изучавахме логически операции. Днес продължаваме да изучаваме логически уравнения и да се учим как да решаваме системи от такива уравнения. Веднага трябва да се отбележи, че системите от логически уравнения се решават малко по-различно от алгебричните. Или по-скоро по други начини.
III. Актуализиране на знанията
– Какво означава да се реши система с две променливи?
Решаването на система с две променливи означава намиране на всички двойки (x, y), които удовлетворяват всяко от дадените уравнения, или доказване, че няма решение.
Какви начини знаете за решаване на системи?
- метод на заместване
- метод на добавяне
- начин за въвеждане на нови променливи,
- графичен метод.
1. Решете система от уравнения в серии.
- Първият ред е чрез добавяне;
- Второто е графично;
- Третият е по метода на заместване.
а) Добавяйки уравнението член по член, имаме: 2 х + 10х = 15 + 9;
12х = 24; х= 2, замествайки тази стойност във второто уравнение, получаваме: 10 . 2 – 11при= 9, откъдето при = 1.
Отговор:(2;1).
б) От първото уравнение, от второто уравнение,

A (2;1) е пресечната точка на графиките на уравненията.
(2;1) – решение на системата.
в) Заместете първото уравнение във второто

11при = 15 – 4, 11при = 11, при = 1.
Отговор: (2;1).
– Какво се нарича скаларно произведение на векторите?
Скаларното произведение на векторите е число, равно на произведението на дължините на тези вектори и косинуса на ъгъла между тях.
Как да напиша точковия продукт в координатна форма?
![]() .
.
IV. Главна сцена
Използвайки две операции „дизюнкция“ и „конюнкция“, разглеждаме булеви системи от две уравнения с две неизвестни:
Намирането на променлива в едно уравнение с една логическа операция води до множество решения. Ако решението на системата беше изразено с някаква конкретна формула, тогава при заместване на първоначалните данни (коефициенти на уравнението) бихме получили напълно определено решение. Използвайки прост пример, виждаме полисемията на решението, следователно или решението на системата в обща форма трябва да бъде изразено с няколко формули, или такива формули не съществуват изрично. Понастоящем такива формули все още не са открити, така че системите от логически уравнения се решават с помощта на уникални методи, с които ще се запознаем днес в урока.
Системата зависи от шест параметъра а,b,° С,д,м,н, всяка от които приема две стойности 0 или 1. Следователно общо получаваме 2 6 = 64 случая.
Аналитичният резултат може да се получи чрез логически разсъждения и преминаване през всички 64 случая.
Упражнение 1.(един ученик работи на дъската).
Решете системата, ако а = 0, b = 0, ° С = 0, д = 0, м = 0, н = 0.
![]() .
.
Отговор:системата има 4 решения: (1;1), (0;1), (1;0),(0;0).
Задача 2.(самостоятелно в тетрадки с последваща проверка).
Решете системата, ако а = 1, b = 0, ° С = 0, д = 0, м = 0, н = 0.
![]() ,
,
Отговор:системата има 2 решения: (0;0), (0;1).
По същия начин можете да разрешите останалите 62 системи, като заместите вместо параметри а,b,° С,д,м,нсъответно стойностите са 0 и 1.
Възможно е дори да се групират някои случаи в класове, за да се подчертаят условия за случаи, когато системата има едно решение, няколко решения или няма решение.
В училищен курс по математика може да се идентифицира много ограничен набор от проблеми, които могат да бъдат решени с помощта на системи от логически уравнения.
Задача 3.Шест прозрачни чаши с вода са подредени в два успоредни реда по три чаши във всяка. Илюстрацията показва изглед отпред и изглед отдясно. През прозрачните стени на чашите се виждат нивата на водата във всяка чаша и във всички чаши зад тях. Определете колко вода се налива във всяка чаша.

На снимката се вижда, че чашите са пълни или празни. Комплектът чаши, които можете да намерите на тези шест места, образува азбука, която се състои от два елемента.
Празна чаша да означим с 0, а пълна с 1. Тогава множеството се състои от 0 и 1, т.е. = (0,1) .
Нека номерираме проекциите на фигурата с числа от 1 до 5.
Нека номерираме редовете очила както следва и да посочим елементите, които могат да се появят в тези редове
Първата проекция показва, че в първата колона няма пълни чаши, т.е. х 11 = 0, х 21 = 0.
От петата проекция става ясно, че х 23 = 0, х 22 = 0. Останалите елементи са лесни за определяне: х 12 = 1, х 13 = 1.
Аналитично формулировката на проблема се свежда до решаване на системата от уравнения

Имаме система от уравнения, в която операциите „+“ са дизюнкция, „ .
" - съчетание.
От второто уравнение на системата и истинските таблици на конюнкция и дизюнкция получаваме х 21 + х 22
+ х 23 = 0 => х 21 = х 22 =
х 23 = 0.
От третото уравнение => х 11 = 0.
Нека заместим намерените стойности на неизвестните в четвъртото и петото уравнения на системата:
Всички свободни и неизвестни членове приемат стойности 0 или 1, а уравненията отговарят на логически операции, т.е. получаваме система от логически уравнения.
По този начин, ако една задача съдържа два вида очила, тогава тя може лесно да бъде решена чрез решаване на система от логически уравнения. Това спестява време и осигурява по-кратко и по-лесно решение.
Нека разгледаме метода на прозрачните таблици (метод на мрежата) - аналог на графичния метод за решаване на алгебрични системи, който ви позволява бързо да решавате система от уравнения, съдържаща не повече от четири променливи.
Този метод се основава на скаларното произведение на векторите.
Тема на урока: Решаване на логически уравнения
Образователни – изучаване на методи за решаване на логически уравнения, развиване на умения за решаване на логически уравнения и конструиране на логически израз с помощта на таблица на истината;развитие - създават условия за развитие на познавателния интерес на учениците, насърчават развитието на паметта, вниманието и логическото мислене;
Образователни : насърчаване на способността да се изслушва мнението на другите,възпитаване на воля и постоянство за постигане на крайни резултати.
Тип урок: комбиниран урок
Оборудване: компютър, мултимедиен проектор, презентация 6.
По време на часовете
Повторение и актуализиране на основни знания. Проверка на домашното (10 минути)
В предишните уроци се запознахме с основните закони на логическата алгебра и се научихме да използваме тези закони за опростяване на логически изрази.
Нека проверим домашното си за опростяване на логически изрази:
1. Коя от следните думи отговаря на логическото условие:
(съгласна първа буква→ съгласна втора буква)٨ (гласна на последната буква → гласна на предпоследната буква)? Ако има няколко такива думи, посочете най-малката от тях.
1) АННА 2) МАРИЯ 3) ОЛЕГ 4) СТЕПАН
Нека въведем следната нотация:
А – първа съгласна буква
Б – съгласна от втора буква
S – гласна последна буква
D – предпоследна гласна буква
Нека направим израз:
Нека направим таблица:
2. Посочете кой логически израз е еквивалентен на израза

Нека опростим записа на оригиналния израз и предложените опции:

3. Даден е фрагмент от таблицата на истинността на израз F:
Кой израз съответства на F?
Нека определим стойностите на тези изрази за посочените стойности на аргументите:
Въведение в темата на урока, представяне на нов материал (30 минути)
Продължаваме да изучаваме основите на логиката и темата на днешния ни урок е „Решаване на логически уравнения“. След изучаването на тази тема ще научите основните начини за решаване на логически уравнения, ще придобиете умения за решаване на тези уравнения с помощта на езика на логическата алгебра и способността да съставяте логически израз с помощта на таблица на истината.
1. Решете логическо уравнение
(¬K M) → (¬L М N) =0
Напишете отговора си като низ от четири знака: стойностите на променливите K, L, M и N (в този ред). Така, например, ред 1101 съответства на факта, че K=1, L=1, M=0, N=1.
Решение:
Нека трансформираме израза(¬K M) → (¬L М Н)
Един израз е неверен, когато и двата термина са неверни. Вторият член е равен на 0, ако M =0, N =0, L =1. В първия член K = 0, тъй като M = 0 и  .
.
Отговор: 0100
2. Колко решения има уравнението (посочете само числото в отговора си)?
Решение: преобразувайте израза
(A +B )*(C +D )=1
A +B =1 и C +D =1
Метод 2: съставяне на таблица на истината
3 начина: изграждане на SDNF - перфектна дизюнктивна нормална форма за функция - дизюнкция на пълни редовни елементарни конюнкции.Нека трансформираме оригиналния израз, отворим скобите, за да получим дизюнкцията на съюзите:
(A+B)*(C+D)=A*C+B*C+A*D+B*D=
Нека допълним съюзите до пълни съюзи (произведението на всички аргументи), отворете скобите:
 Нека вземем предвид същите връзки:
Нека вземем предвид същите връзки:
В резултат на това получаваме SDNF, съдържащ 9 конюнкции. Следователно таблицата на истината за тази функция има стойност 1 в 9 реда от 2 4 =16 набора от стойности на променливи.
3. Колко решения има уравнението (посочете само числото в отговора си)?

Нека опростим израза:
 ,
,
3 начина: изграждане на SDNF
Нека вземем предвид същите връзки:
В резултат на това получаваме SDNF, съдържащ 5 конюнкции. Следователно таблицата на истината за тази функция има стойност 1 на 5 реда от 2 4 =16 набора от стойности на променливи.
Конструиране на логически израз с помощта на таблица на истината:
за всеки ред от таблицата на истината, съдържащ 1, съставяме произведение от аргументи и променливи, равни на 0, се включват в произведението с отрицание, а променливи, равни на 1, се включват без отрицание. Желаният израз F ще бъде съставен от сумата на получените продукти. След това, ако е възможно, този израз трябва да бъде опростен.
Пример: дадена е таблица на истинност на израз. Конструирайте логически израз.
Решение:3. Домашна работа (5 минути)
Решете уравнението:
Колко решения има уравнението (посочете само числото в отговора си)?
Използвайки дадена таблица на истинност, съставете логически израз и
опростете го.