Перпендикулярни линии се появяват в почти всяка геометрична задача. Понякога перпендикулярността на правите е известна от условието, а в други случаи перпендикулярността на правите трябва да се докаже. За да се докаже перпендикулярността на две прави линии, достатъчно е да се покаже, използвайки всякакви геометрични методи, че ъгълът между правите линии е равен на деветдесет градуса.
Как да отговоря на въпроса „правите перпендикулярни ли са“, ако са известни уравненията, които определят тези линии в равнина или в триизмерно пространство?
За да направите това, трябва да използвате необходимо и достатъчно условие за перпендикулярност на две прави. Нека го формулираме под формата на теорема.
Теорема.
аИ bнеобходимо и достатъчно е векторът на посоката да е прав абеше перпендикулярен на насочващия вектор на правата линия b.
Доказателството на това условие за перпендикулярност на правите се основава на дефиницията на насочващия вектор на правата и на дефиницията на перпендикулярните прави.
Да добавим конкретика.
Нека на равнината е въведена правоъгълна декартова координатна система Оксии са дадени уравненията на права върху равнина от някакъв тип, определящи линиите аИ b. Нека обозначим векторите на посоката на правите АИ bкакто и съответно. Чрез уравнения на прави аИ bможем да определим координатите на насочващите вектори на тези прави - получаваме и . След това, за перпендикулярността на линиите аИ bНеобходимо и достатъчно е условието за перпендикулярност на векторите и да е изпълнено, тоест скаларното произведение на векторите и да е равно на нула: 
.
Така, аИ bв правоъгълна координатна система Оксина равнината има формата , където и са векторите на посоката на линиите аИ bсъответно.
Това условие е удобно за използване, когато координатите на насочващите вектори на прави линии се намират лесно, а също и когато правите линии аИ bсъответстват на канонични уравнения на права върху равнина или параметрични уравнения на права върху равнина.
Пример.
В правоъгълна координатна система Оксидават се три точки. Перпендикулярни ли са линиите? ABИ AC?
Решение.
Векторите и са векторите на посоката на правите ABИ AC. Позовавайки се на координатите на статията на вектор въз основа на координатите на началната и крайната му точка, ние изчисляваме 
. Вектори и са перпендикулярни, тъй като 
. Така необходимото и достатъчно условие за перпендикулярност на правите е изпълнено ABИ AC. Следователно, направо ABИ ACперпендикулярен.
Отговор:
Да, правите линии са перпендикулярни.
Пример.
Дали правите и 
перпендикулярно?
Решение.
Насочващият вектор е права линия и е насочващият вектор на права линия . Нека изчислим скаларното произведение на векторите и: 
. Той е различен от нула, следователно векторите на посоката на линиите не са перпендикулярни. Това означава, че условието за перпендикулярност на линиите не е изпълнено, следователно оригиналните линии не са перпендикулярни.
Отговор:
не, линиите не са перпендикулярни.
по същия начин, необходимо и достатъчно условие за перпендикулярност на линиите аИ bв правоъгълна координатна система Oxyzв триизмерното пространство има формата 
, Където 
И 
- насочващи вектори на прави линии аИ bсъответно.
Пример.
Перпендикулярни ли са линиите, определени в правоъгълна координатна система? Oxyzв триизмерното пространство чрез уравнения 
И ?
Решение.
Числата в знаменателите на каноничните уравнения на права в пространството са съответните координати на насочващия вектор на правата. А координатите на насочващия вектор на правата, който се задава от параметричните уравнения на правата в пространството, са коефициентите на параметъра. По този начин, 
и са насочващите вектори на дадените прави линии. Нека разберем дали са перпендикулярни: 
. Тъй като скаларното произведение е нула, тези вектори са перпендикулярни. Това означава, че условието за перпендикулярност на дадените прави е изпълнено.
Отговор:
правите линии са перпендикулярни.
За проверка на перпендикулярността на две прави в една равнина има други необходими и достатъчни условия за перпендикулярност.
Теорема.
За перпендикулярност на линиите аИ bна равнината е необходимо и достатъчно нормалният вектор да е права линия абеше перпендикулярен на нормалния вектор на правата b.
Посоченото условие за перпендикулярност на линиите е удобно за използване, ако с помощта на дадените уравнения на линиите могат лесно да се намерят координатите на нормалните вектори на линиите. Това твърдение съответства на общото уравнение на правата линия на формата 
, уравнението на права в сегменти и уравнението на права с ъглов коефициент.
Пример.
Уверете се, че е прав 
и перпендикулярно.
Решение.
Като се имат предвид уравненията на линиите, лесно е да се намерят координатите на нормалните вектори на тези линии. – вектор на нормална линия . Нека пренапишем уравнението във формата 
, откъдето се виждат координатите на нормалния вектор на тази права: .
Векторите и са перпендикулярни, тъй като тяхното скаларно произведение е равно на нула: 
. Така е изпълнено необходимото и достатъчно условие за перпендикулярност на дадените прави, тоест те са наистина перпендикулярни.
По-специално, ако е директно ана равнината определя уравнението на права линия с ъглов коефициент от формата , а правата линия b– от вида , то нормалните вектори на тези прави имат съответно координати и , а условието за перпендикулярност на тези прави се свежда до следната връзка между ъгловите коефициенти .
Пример.
Правите и перпендикулярни ли са?
Решение.
Наклонът на права линия е равен на , а наклонът на права линия е равен на . Произведението на ъгловите коефициенти е равно на минус едно, следователно линиите са перпендикулярни.
Отговор:
дадените прави са перпендикулярни.
Може да се посочи още едно условие за перпендикулярност на правите в равнина.
Теорема.
За перпендикулярност на линиите аИ bна равнина е необходимо и достатъчно насочващият вектор на една права и нормалният вектор на втората права да са колинеарни.
Това условие очевидно е удобно за използване, когато координатите на насочващия вектор на една права и координатите на нормалния вектор на втората права се намират лесно, т.е. когато една права е дадена от канонично уравнение или параметрични уравнения на права на равнина, а вторият или чрез общо уравнение на права, или уравнение на права в сегменти, или уравнение на права линия с ъглов коефициент.
Пример.
Прави линии и перпендикулярни ли са?
Решение.
Очевидно е нормалният вектор на правата и е векторът на посоката на правата. Векторите и не са колинеарни, тъй като за тях условието за колинеарност на два вектора не е изпълнено (няма такова реално число T, при което). Следователно дадените прави не са перпендикулярни.
Отговор:
линиите не са перпендикулярни.
21. Разстояние от точка до права.
Разстоянието от точка до линия се определя от разстоянието от точка до точка. Нека покажем как се прави.
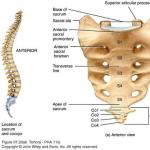
Нека е дадена права линия на равнина или в триизмерно пространство аи точка М 1, а не по права линия а. Нека начертаем през точката М 1директен b, перпендикулярна на правата а. Нека означим пресечната точка на правите аИ bкак H 1. Линеен сегмент M 1 H 1Наречен перпендикулярен, изтеглен от точката М 1към права линия а.
Определение.
Разстояние от точката М 1към права линия а наричаме разстоянието между точките М 1И H 1.
Въпреки това, най-често срещаната дефиниция на разстоянието от точка до права е дължината на перпендикуляра.
Определение.
Разстояние от точка до линияе дължината на перпендикуляра, прекаран от дадена точка към дадена права.
Това определение е еквивалентно на първото определение на разстоянието от точка до права.
Моля, обърнете внимание, че разстоянието от точка до линия е най-малкото от разстоянията от тази точка до точките на дадена линия. Нека го покажем.
Нека го вземем на права линия аточка Q, несъвпадащ с точката М 1. Линеен сегмент M 1 QНаречен наклонен, изтеглен от точката М 1към права линия а. Трябва да покажем, че перпендикулярът, прекаран от точката М 1към права линия а, по-малко от всеки наклон, изчертан от точката М 1към права линия а. Вярно е: триъгълник M 1 QH 1правоъгълник с хипотенуза M 1 Q, а дължината на хипотенузата винаги е по-голяма от дължината на който и да е от катетите, следователно, 
.
22. Равнина в пространството R3. Уравнение на равнина.
Равнина в декартова правоъгълна координатна система може да бъде дадена с уравнението, 
което се нарича общо уравнениесамолет.
Определение.Векторът е перпендикулярен на равнината и се нарича неин нормален вектор.
Ако в правоъгълна координатна система са известни координатите на три точки, които не лежат на една права, тогава уравнението на равнината се записва като: 
.
След като изчислим тази детерминанта, получаваме общото уравнение на равнината.
Пример.Напишете уравнението на равнината, минаваща през точките.
Решение:
Уравнение на равнината: .
23. Изследване на общото уравнение на равнината.
Определение 2. Всеки вектор, перпендикулярен на равнина, се нарича нормален вектор на тази равнина.
Ако е известна фиксирана точка М 0 (х 0 , г 0 , z 0), лежаща в дадена равнина, а векторът е перпендикулярен на дадена равнина, тогава уравнението на равнината, минаваща през точката М 0 (х 0 , г 0 , z 0), перпендикулярен на вектора, има формата
А(х-х 0)+Б(у-у 0)+C(z-z 0)= 0. (3.22)
Нека покажем, че уравнение (3.22) е общото уравнение на равнината (3.21). За да направите това, отворете скобите и поставете свободния термин в скоби:
.Axe + By+ Cz +(-Брадва 0 -От-Cz 0)= 0
Като определи д = -Брадва 0 -От-Cz 0, получаваме уравнението Ax + By + Cz + D= 0.
Задача 1.Напишете уравнение за равнина, минаваща през точка А, перпендикулярна на вектора, ако А(4, -3, 1), б(1, 2, 3).
Решение.Нека намерим нормалния вектор на равнината:
За да намерим уравнението на равнината, използваме уравнение (3.22):
Отговор: -3х + 5г + 2z + 25 = 0.
Задача 2.Напишете уравнение за равнина, минаваща през точка М 0 (-1, 2, -1), перпендикулярно на оста OZ.
Решение.Като нормален вектор на желаната равнина можете да вземете всеки вектор, лежащ върху оста OZ, например, след това уравнението на равнината
Отговор: z + 1 = 0.
24. Разстояние от точка до равнина.
Разстоянието от точка до равнина се определя чрез разстоянието от точка до точка, едното от които е дадена точка, а другото е проекцията на дадена точка върху дадена равнина.
Нека е дадена точка в триизмерното пространство М 1и самолет. Нека начертаем през точката М 1директен а, перпендикулярна на равнината. Нека означим пресечната точка на правата аи самолети като H 1. Линеен сегмент M 1 H 1Наречен перпендикулярен, отпадна от точката М 1до равнина и точка H 1 – основа на перпендикуляра.
Определение.
е разстоянието от дадена точка до основата на перпендикуляр, прекаран от дадена точка към дадена равнина.
Най-често срещаната дефиниция на разстоянието от точка до равнина е следната.
Определение.
Разстояние от точка до равнинае дължината на перпендикуляра, прекаран от дадена точка към дадена равнина.
Трябва да се отбележи, че разстоянието от точката М 1до така определената равнина е най-малкото от разстоянията от дадена точка М 1до всяка точка на самолета. Наистина, нека точката H 2лежи в равнината и е различна от точката H 1. Очевидно триъгълник M 2 H 1 H 2е правоъгълна, в нея M 1 H 1– крак и M 1 H 2– хипотенуза, следователно, 
. Между другото, сегментът M 1 H 2Наречен наклонен, изтеглен от точката М 1до самолета. И така, перпендикуляр, прекаран от дадена точка към дадена равнина, винаги е по-малък от наклонен, прекаран от същата точка към дадена равнина.
Ако една права минава през две дадени точки ,
после нея уравнениетонаписана във формуляра : 
.
Определение.Векторът се нарича водачивектор на права, ако е успореден или й принадлежи.
Пример.Напишете уравнението на права, минаваща през две дадени точки 
.
Решение: Използваме общата формула на права, минаваща през две дадени точки: - канонично уравнение на права, минаваща през точки и . Векторът е вектор с права посока.
26. Относително разположение на линиите в пространството R3.
Нека да преминем към опциите за взаимното разположение на две линии в пространството.
Първо, две прави могат да съвпадат, тоест да имат безкрайно много общи точки (поне две общи точки).
Второ, две прави в пространството могат да се пресичат, тоест да имат една обща точка. В този случай тези две линии лежат в някаква равнина на триизмерното пространство. Ако две прави се пресичат в пространството, тогава стигаме до концепцията за ъгъл между пресичащите се прави.
Трето, две прави в пространството могат да бъдат успоредни. В този случай те лежат в една равнина и нямат общи точки. Препоръчваме ви да проучите статията успоредни прави, успоредност на прави.
След като дадохме дефиницията на успоредни прави в пространството, трябва да поговорим за насочващите вектори на права линия поради тяхната важност. Всеки ненулев вектор, лежащ на тази права или на права, която е успоредна на тази, ще се нарича вектор на посоката на правата. Векторът на посоката на права линия много често се използва при решаване на задачи, включващи права линия в пространството.
И накрая, две линии в триизмерното пространство могат да се пресичат. Две прави в пространството се наричат коси, ако не лежат в една и съща равнина. Това взаимно разположение на две прави линии в пространството ни води до концепцията за ъгъл между пресичащи се прави линии.
От особено практическо значение е случаят, когато ъгълът между пресичащи се или пресичащи се линии в триизмерното пространство е равен на деветдесет градуса. Такива линии се наричат перпендикулярни (вижте статията перпендикулярни линии, перпендикулярност на линиите).
27. Относителното разположение на права линия и равнина в пространството R3.
Една права линия може да лежи на дадена равнина, да бъде успоредна на дадена равнина или да я пресича в една точка, вижте следващите фигури.
Ако , то това означава, че . И това е възможно само когато правата лежи на равнината или е успоредна на нея. Ако една права лежи на равнина, тогава всяка точка от правата е точка от равнината и координатите на всяка точка от правата удовлетворяват уравнението на равнината. Следователно е достатъчно да се провери дали точката лежи на равнината. Ако , тогава точка 
- лежи на равнината, което означава, че самата права лежи на равнината.
Ако , a , то точката от правата не лежи на равнината, което означава, че правата е успоредна на равнината.
Теоремата е доказана.
В този урок ще повторим теорията и ще докажем теоремата, която показва перпендикулярността на права и равнина.
В началото на урока нека си припомним определението за права, перпендикулярна на равнина. След това ще разгледаме и докажем теоремата, която показва перпендикулярността на права и равнина. За да докажете тази теорема, припомнете си свойството на перпендикулярната ъглополовяща.
След това ще решим няколко задачи за перпендикулярността на права и равнина.
Тема: Перпендикулярност на права и равнина
Урок: Признак за перпендикулярност на права и равнина
В този урок ще повторим теорията и ще докажем теорема-тест за перпендикулярност на права и равнина.
Определение. Направо Асе нарича перпендикулярна на равнината α, ако е перпендикулярна на всяка права, лежаща в тази равнина.
Ако една права е перпендикулярна на две пресичащи се прави, лежащи в равнина, то тя е перпендикулярна на тази равнина.
Доказателство.
Нека ни е дадена равнина α. В тази равнина има две пресичащи се прави стрИ р. Направо Аперпендикулярно на права линия стри прав р. Трябва да докажем, че линията Ае перпендикулярна на равнината α, тоест тази права a е перпендикулярна на всяка права, лежаща в равнината α.
Напомняне.
За да докажем това, трябва да си припомним свойствата на ъглополовящата на отсечка. Перпендикулярна ъглополовяща Ркъм сегмента AB- това е геометричното място на точките, еднакво отдалечени от краищата на сегмента. Това е, ако точката СЪСлежи на ъглополовящата p, тогава AC = BC.
Нека точката ОТНОСНО- точка на пресичане на линията Аи равнина α (фиг. 2). Без загуба на общост ще приемем, че правите линии стрИ рпресичат се в точка ОТНОСНО. Трябва да докажем перпендикулярността на правата Акъм произволна линия мот равнината α.
Нека начертаем през точката ОТНОСНОдиректен л, успоредна на правата м.На права линия Анека оставим настрана сегментите ОАИ ОВ, и ОА = ОВ, тоест точката ОТНОСНО- средата на сегмента AB. Да направим директен П.Л., 
.
Направо Рперпендикулярно на права линия А(от условието), 
(по конструкция). означава, Р AB. Точка Рлежи на права линия Р. означава, RA = PB.
Направо рперпендикулярно на права линия А(от условието), 
(по конструкция). означава, р- ъглополовяща на отсечка AB. Точка Qлежи на права линия р. означава, QA =QB.
Триъгълници ARQИ VRQравни от три страни (RA = PB, QA =QB, PQ-обща страна). Така че ъглите ARQИ VRQса равни.
Триъгълници АП.Л.И BPLравен по ъгъл и две съседни страни (∠ ARЛ= ∠VRL, RA = PB, П.Л.- обща страна). От равенството на триъгълниците получаваме това AL =Б.Л..
Помислете за триъгълник ABL.Той е равнобедрен, защото AL =БЛ.В равнобедрен триъгълник медианата LОе и височината, тоест права линия LОперпендикулярен AB.
Разбрахме това Аперпендикулярно на права линия л,и следователно директен м, Q.E.D.
Точки А, М, Олежат на права, перпендикулярна на равнината α, а точките О, V, SИ длежат в равнината α (фиг. 3). Кои от следните ъгли са прави: ?
Решение
Нека разгледаме ъгъла. Направо АДперпендикулярна на равнината α и следователно права линия АДперпендикулярна на всяка права, лежаща в равнината α, включително правата IN. Означава,.
Нека разгледаме ъгъла. Направо АДперпендикулярно на права линия операционна система, Означава,.
Нека разгледаме ъгъла. Направо АДперпендикулярно на права линия ОТНОСНОд, Означава,. Помислете за триъгълник DAO. Триъгълникът може да има само един прав ъгъл. Така че ъгълът ДАМ- не е директен.
Нека разгледаме ъгъла. Направо АДперпендикулярно на права линия ОТНОСНОд, Означава,.
Нека разгледаме ъгъла. Това е ъгъл в правоъгълен триъгълник BMO, не може да бъде прав, тъй като ъгълът меморандум за разбирателство- прав.
Отговор: 
.
В триъгълник ABCдадено: , AC= 6 см, слънце= 8 см, СМ- медиана (фиг. 4). През върха СЪСбеше начертана пряка линия SK, перпендикулярна на равнината на триъгълника ABC, и SK= 12 см Намерете КМ.
Решение:
Нека намерим дължината ABспоред Питагоровата теорема: (cm).
Според свойството на правоъгълен триъгълник средата на хипотенузата е Мна еднакво разстояние от върховете на триъгълника. Това е SM = AM = VM, 
(см).
Помислете за триъгълник KSM. Направо KSперпендикулярна на равнината ABC, което означава KSперпендикулярен СМ. Така че това е триъгълник KSM- правоъгълен. Нека намерим хипотенузата КМот Питагоровата теорема: (cm).
1. Геометрия. 10-11 клас: учебник за ученици от общообразователни институции (основни и специализирани нива) / I. M. Smirnova, V. A. Smirnov. - 5-то издание, коригирано и разширено - М.: Мнемозина, 2008. - 288 с.: ил.
Задачи 1, 2, 5, 6 стр. 57
2. Определете перпендикулярността на права и равнина.
3. Посочете двойка в куба - ръб и лице, които са перпендикулярни.
4. Точка ДА СЕлежи извън равнината на равнобедрен триъгълник ABCи на еднакво разстояние от точките INИ СЪС. М- средата на основата слънце. Докажете, че линията слънцеперпендикулярна на равнината АКМ.
Права линия (сегмент от права линия) се обозначава с две главни букви от латинската азбука или една малка буква. Точката се обозначава само с главна латинска буква.
Линиите не могат да се пресичат, пресичат или съвпадат. Пресичащите се прави имат само една обща точка, непресичащите се нямат обща точка, а съвпадащите имат всички общи точки.
Определение. Две прави, пресичащи се под прав ъгъл, се наричат перпендикулярни. Перпендикулярността на правите линии (или техните сегменти) се обозначава със знака за перпендикулярност „⊥“.
Например:
Вашият ABИ CD(фиг. 1) се пресичат в точката ОТНОСНОи ∠ AOC = ∠ВОС = ∠AOD = ∠БПК= 90°, тогава AB ⊥ CD.
Ако AB ⊥ CD(фиг. 2) и се пресичат в т IN, тогава ∠ ABC = ∠ABD= 90°
Свойства на перпендикулярните прави
1. През точка А(фиг. 3) може да се начертае само една перпендикулярна права линия ABкъм права линия CD;останалите прави, минаващи през точката Аи пресичане CD, се наричат наклонени прави линии (фиг. 3, прави линии AEИ AF).
2. От точка Аможете да спуснете перпендикуляра до права линия CD; перпендикулярна дължина (дължина на сегмента AB), изтеглен от точката Адиректно CD, е най-късото разстояние от Апреди CD(фиг. 3).
В този урок ще повторим теорията и ще докажем теоремата, която показва перпендикулярността на права и равнина.
В началото на урока нека си припомним определението за права, перпендикулярна на равнина. След това ще разгледаме и докажем теоремата, която показва перпендикулярността на права и равнина. За да докажете тази теорема, припомнете си свойството на перпендикулярната ъглополовяща.
След това ще решим няколко задачи за перпендикулярността на права и равнина.
Тема: Перпендикулярност на права и равнина
Урок: Признак за перпендикулярност на права и равнина
В този урок ще повторим теорията и ще докажем теорема-тест за перпендикулярност на права и равнина.
Определение. Направо Асе нарича перпендикулярна на равнината α, ако е перпендикулярна на всяка права, лежаща в тази равнина.
Ако една права е перпендикулярна на две пресичащи се прави, лежащи в равнина, то тя е перпендикулярна на тази равнина.
Доказателство.
Нека ни е дадена равнина α. В тази равнина има две пресичащи се прави стрИ р. Направо Аперпендикулярно на права линия стри прав р. Трябва да докажем, че линията Ае перпендикулярна на равнината α, тоест тази права a е перпендикулярна на всяка права, лежаща в равнината α.
Напомняне.
За да докажем това, трябва да си припомним свойствата на ъглополовящата на отсечка. Перпендикулярна ъглополовяща Ркъм сегмента AB- това е геометричното място на точките, еднакво отдалечени от краищата на сегмента. Това е, ако точката СЪСлежи на ъглополовящата p, тогава AC = BC.
Нека точката ОТНОСНО- точка на пресичане на линията Аи равнина α (фиг. 2). Без загуба на общост ще приемем, че правите линии стрИ рпресичат се в точка ОТНОСНО. Трябва да докажем перпендикулярността на правата Акъм произволна линия мот равнината α.
Нека начертаем през точката ОТНОСНОдиректен л, успоредна на правата м.На права линия Анека оставим настрана сегментите ОАИ ОВ, и ОА = ОВ, тоест точката ОТНОСНО- средата на сегмента AB. Да направим директен П.Л., .
Направо Рперпендикулярно на права линия А(от условието), (по конструкция). означава, Р AB. Точка Рлежи на права линия Р. означава, RA = PB.
Направо рперпендикулярно на права линия А(от условието), (по конструкция). означава, р- ъглополовяща на отсечка AB. Точка Qлежи на права линия р. означава, QA =QB.
Триъгълници ARQИ VRQравни от три страни (RA = PB, QA =QB, PQ-обща страна). Така че ъглите ARQИ VRQса равни.
Триъгълници АП.Л.И BPLравен по ъгъл и две съседни страни (∠ ARЛ= ∠VRL, RA = PB, П.Л.- обща страна). От равенството на триъгълниците получаваме това AL =Б.Л..
Помислете за триъгълник ABL.Той е равнобедрен, защото AL =БЛ.В равнобедрен триъгълник медианата LОе и височината, тоест права линия LОперпендикулярен AB.
Разбрахме това Аперпендикулярно на права линия л,и следователно директен м, Q.E.D.
Точки А, М, Олежат на права, перпендикулярна на равнината α, а точките О, V, SИ длежат в равнината α (фиг. 3). Кои от следните ъгли са прави: ?
Решение
Нека разгледаме ъгъла. Направо АДперпендикулярна на равнината α и следователно права линия АДперпендикулярна на всяка права, лежаща в равнината α, включително правата IN. Означава,.
Нека разгледаме ъгъла. Направо АДперпендикулярно на права линия операционна система, Означава,.
Нека разгледаме ъгъла. Направо АДперпендикулярно на права линия ОТНОСНОд, Означава,. Помислете за триъгълник DAO. Триъгълникът може да има само един прав ъгъл. Така че ъгълът ДАМ- не е директен.
Нека разгледаме ъгъла. Направо АДперпендикулярно на права линия ОТНОСНОд, Означава,.
Нека разгледаме ъгъла. Това е ъгъл в правоъгълен триъгълник BMO, не може да бъде прав, тъй като ъгълът меморандум за разбирателство- прав.
Отговор: .
В триъгълник ABCдадено: , AC= 6 см, слънце= 8 см, СМ- медиана (фиг. 4). През върха СЪСбеше начертана пряка линия SK, перпендикулярна на равнината на триъгълника ABC, и SK= 12 см Намерете КМ.
Решение:
Нека намерим дължината ABспоред Питагоровата теорема: (cm).
Според свойството на правоъгълен триъгълник средата на хипотенузата е Мна еднакво разстояние от върховете на триъгълника. Това е SM = AM = VM, (см).
Помислете за триъгълник KSM. Направо KSперпендикулярна на равнината ABC, което означава KSперпендикулярен СМ. Така че това е триъгълник KSM- правоъгълен. Нека намерим хипотенузата КМот Питагоровата теорема: (cm).
1. Геометрия. 10-11 клас: учебник за ученици от общообразователни институции (основни и специализирани нива) / I. M. Smirnova, V. A. Smirnov. - 5-то издание, коригирано и разширено - М.: Мнемозина, 2008. - 288 с.: ил.
Задачи 1, 2, 5, 6 стр. 57
2. Определете перпендикулярността на права и равнина.
3. Посочете двойка в куба - ръб и лице, които са перпендикулярни.
4. Точка ДА СЕлежи извън равнината на равнобедрен триъгълник ABCи на еднакво разстояние от точките INИ СЪС. М- средата на основата слънце. Докажете, че линията слънцеперпендикулярна на равнината АКМ.
Предварителна информация за директен
Понятието права линия, както и понятието точка, са основните понятия на геометрията. Както знаете, основните понятия не са дефинирани. Това не е изключение от концепцията за права линия. Затова нека разгледаме същността на това понятие чрез неговото изграждане.
Вземете линийка и, без да вдигате молива си, начертайте линия с произволна дължина. Ще наречем получената линия права линия. Тук обаче трябва да се отбележи, че това не е цялата права линия, а само част от нея. Самата права линия е безкрайна в двата си края.
Правите линии ще обозначаваме с малка латинска буква или нейните две точки в скоби (фиг. 1).
Понятията права линия и точка са свързани с три аксиоми на геометрията:
Аксиома 1:За всяка произволна права има поне две точки, които лежат на нея.
Аксиома 2:Можете да намерите поне три точки, които не лежат на една права.
Аксиома 3:Една права линия винаги минава през 2 произволни точки и тази права линия е уникална.
За две прави линии относителната им позиция е от значение. Възможни са три случая:
- Две прави линии съвпадат. В този случай всяка точка от една права ще бъде и точка от другата права.
- Две линии се пресичат. В този случай само една точка от една права ще принадлежи и на другата права.
- Две прави са успоредни. В този случай всяка от тези линии има свой собствен набор от точки, които са различни една от друга.
Перпендикулярност на линиите
Да разгледаме две произволни пресичащи се прави. Очевидно в точката на тяхното пресичане се образуват 4 ъгъла. Тогава
Определение 1
Ще наричаме пресичащите се прави перпендикулярни, ако поне един ъгъл, образуван от тяхното пресичане, е равен на $90^0$ (фиг. 2).
Обозначение: $a⊥b$.
Помислете за следния проблем:
Пример 1
Намерете ъгли 1, 2 и 3 от фигурата по-долу
Следователно ъгъл 2 е вертикален за дадения ни ъгъл
Следователно ъгъл 1 е съседен на ъгъл 2
$∠1=180^0-∠2=180^0-90^0=90^0$
Следователно ъгъл 3 е вертикален спрямо ъгъл 1
$∠3=∠1=90^0$
От този проблем можем да направим следната забележка
Бележка 1
Всички ъгли между перпендикулярни прави са равни на $90^0$.
Основна теорема за перпендикулярните прави
Нека въведем следната теорема:
Теорема 1
Две линии, които са перпендикулярни на третата, ще се разминават.
Доказателство.
Нека да разгледаме фигура 3 според условията на проблема.
Нека мислено разделим тази фигура на две части от правата $(ZP)$. Нека поставим дясната страна върху лявата. Тогава, тъй като правите $(NM)$ и $(XY)$ са перпендикулярни на правата $(PZ)$ и следователно ъглите между тях са прави, лъчът $NP$ ще бъде насложен изцяло върху лъча $ PM$ и лъчът $XZ $ ще бъде насложен изцяло върху лъча $YZ$.
Сега да предположим обратното: нека тези линии се пресичат. Без да губим общост, нека приемем, че те се пресичат от лявата страна, т.е. нека лъчът $NP$ се пресича с лъча $YZ$ в точка $O$. Тогава, съгласно описаната по-горе конструкция, ще получим, че лъчът $PM$ се пресича с лъча $YZ$ в точката $O"$. Но тогава получаваме, че през две точки $O$ и $O"$, има две прави линии $(NM)$ и $(XY)$, което противоречи на аксиомата за 3 прави линии.
Следователно правите $(NM)$ и $(XY)$ не се пресичат.
Теоремата е доказана.
Примерна задача
Пример 2
Дадени са две прави, които имат пресечна точка. През точка, която не принадлежи на никоя от тях, са прекарани две прави, едната от които е перпендикулярна на една от описаните по-горе прави, а другата е перпендикулярна на другата от тях. Докажете, че не са еднакви.
Нека начертаем картина според условията на задачата (фиг. 4).
От условията на задачата ще имаме, че $m⊥k,n⊥l$.
Да приемем обратното, нека правите $k$ и $l$ съвпадат. Нека е прав $l$. Тогава, по условие, $m⊥l$ и $n⊥l$. Следователно, съгласно теорема 1, правите $m$ и $n$ не се пресичат. Получихме противоречие, което означава, че правите $k$ и $l$ не съвпадат.
